The integral of csc(x)

Dec17

[NOTE: At the end of editing this, I found that the substitution used below is famous enough to have a name, and for Spivak to have called it the “world’s sneakiest substitution”. Glad I’m not the only one who thought so.]

In the course of working through some (very good) material on neural networks (which I may try to work through here later), I noticed that it was beneficial for a so-called “activation function” to be able to be written as the solution of an “easy” differential equation. Here by “easy” I mean something closer to “short to write” than “easy to solve”.

The [activation] function sigma.

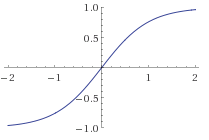
In particular, two often used activation functions are
$\sigma (x) := \frac{1}{1+e^{-t}}$
and
$\tau (x) := \tanh{x} = \frac{e^{2x}-1}{e^{2x}+1}.$

One might observe that these satisfy the equations
$\sigma' = \sigma (1-\sigma),$
and
$\tau' = 1-\tau^2.$

By invoking some theorems of Picard, Lindelof, Cauchy and Lipschitz (I was only going to credit Picard until wikipedia set me right), we recall that we could start from these (separable) differential equations and fix a single point to guarantee we would end up at the functions above. In seeking to solve the second, I found after substituting cos(u) =τ that
$-\int\frac{du}{\sin{u}} = x+C,$
and shortly after that, I realized I had no idea how to integrate csc(u). Obviously the internet knows (substitute v = cot(u) + csc(u) to get the integral being –log(cot(u)+csc(u))), which is a really terrible answer, since I would never have gotten there myself.

Not the right approach.

Instinctually, I might have tried the approach to the right, which gets you back to where we started, or by changing the numerator to cos²x+sin²x, which leads to some amount of trouble, though intuitively, this feels like the right way to do it. Indeed, eventually this might lead you to using half angles (and avoiding integrals of inverse trig functions). We find
$I = \int \frac{du}{\sin{u}} = \int \frac{\cos^2{u/2} + \sin^2{u/2}}{2\cos{u/2}\sin{u/2}}.$
Avoiding the overwhelming temptation to split this integral into summands (which would leave us with a cot(u)), we instead divide the numerator and denominator by sin²(u) to find
$I=\int \frac{1+\tan^2{u/2}}{2\tan{u/2}} du.$
Now substituting v = tan(u/2), we find that dv = 1/2 (1+tan²(u/2))du = 1/2(1+v²)du, so making this substitution, and then undoing all our old substitutions:
$I = \int \frac{1+v^2}{v}*\frac{2}{1+v^2}dv = \int \frac{dv}{v} = \log{|v|} + C = \log{|\tan{\frac{u}{2}}|}+C = \log{|\tan{\frac{\cos^{-1}\tau}{2}}|}+C.$

The function tau we worry so much about. Looks pretty much like sigma.

Using the half angle formulae that everyone of course remembers and dropping the C (remember, there’s already a constant on the other side of this equation), this simplifies to (finally)
$I = \log{|\frac{\sqrt{1-\tau^2}}{1+\tau}|}.$ Subbing back in and solving for $\tau(x)$ gives, as desired,

$\tau(x) = \frac{e^{2x}-1}{1+e^{2x}}$ .

Phew.

Expectations II

Mar13

A contour plot of the function. Pretty respectable looking hills- maybe somewhere in the Ozarks- if I say so myself.

As a further example of yesterday’s post, I was discussing multivariable calculus with a student who had never taken it, and mentioned the gradient. Putting our discussion into the framework of this post, here is what he wanted out of such a high dimensional analogue of the derivative of a function $f: \mathbb{R}^2 \to \mathbb{R}$ (note to impressionable readers: the function defined below is not quite the gradient):
1. Name the answer: Call the gradient D.
2. Describe the answer: D should be a function from $\mathbb{R}^2 \times \mathbb{R}^2 \to \mathbb{R}^3$ , which takes a point in the domain, a direction in the domain, and returns the vector in the range. The idea being that if you had a map, knew where you are and in which direction you wished to travel, then the gradient should tell you what 3-dimensional direction you would head off in.

Certainly there is such a function, though in some sense we are making it too complicated. As an example we have some pictures of the beautiful hills formed by the function

$f(x,y) = \sin{3y} + \sin{(4x + 5y)} - x^2 - y^2 + 4.$

The (actual) gradient of this function is

$\nabla f(x,y) = \left(4\cos (4x + 5y) - 2x, 3\cos(3y) - 2y + 5\cos(4x + 5y)\right)$ .
Plugging in a point in the plane will give a single vector, and then taking the dot product of this vector with a direction will give a rate of change for f at that point, in that direction. Specifically, if we start walking north at unit speed from the origin, the gradient will be (4,8), and I take the dot product of this with (0,1) to find that I will be climbing at 8m/s (depending on our units!)

Now the correct answer from my student’s point of view would be that the answer is (0,1,8), since this is the direction in 3 dimensions that one would travel, and that the correct definition for D would have
$Df(x,y) \cdot v = \left(x,y,\nabla(x,y) \cdot v \right)$ .

The graph of the indicated function, including the vector of the "pseudo-gradient" we discuss.

Of course there are more sophisticated examples of this. Suppose a function $u: \mathbb{R}^n \to \mathbb{R}$ is harmonic. That is to say, $\Delta u := \sum_{j = 1}^n \frac{\partial^2 u}{\partial x_j^2} = 0$ . Notice that in order to write down this equality, we already named our solution u. But just working from this equation, we can deduce a number of qualities that any solution must have: u is infinitely differentiable and, restricted to any compact set, attains its maximum and minimum on the boundary of that set. Such properties quickly allow us to narrow down the possibilities for solutions to problems.

A picture of some hills that might be shaped like the function we're looking at. In the Ozarks of all places!

Math-ing the place up

Mar8

A convex function, with one secant line drawn in red.

Haven’t had a straight up “math” day in quite a while here. That ends now. While reading an article [PDF link], I came across the definition of a Young function: a function $F: [0,\infty) \to [0,\infty)$ which is convex and where F(t) = 0 only when t = 0. Recall that for a real valued function, convex means that every secant line lies above the curve. So far, so good. Such a function might serve as a measure of how alike two functions are: rather than looking at (for example) the $L^2$ norm of u-v, we might first see what we can say about F(|u-v|), a more general question.

But here’s the proposition that made me pause: For 1<q<m<p, there is a differentiable Young function F and a constant C(m,p,q)>0 so that

1. $\int_0^{\infty}F'(t)^{-\frac{1}{m-1}}~dt\leq C$ , and

2. $q\leq \frac{tF'(t)}{F(t)}\leq p$ for all t > 0.

A non-convex function, with a secant line drawn in passing beneath the function.

In fact, there was one more somewhat technical, but non-trivial assertion about this F (proposition 2.1 in the linked paper), but let’s focus on these two. Initially I was convinced that no such F existed, even satisfying these two conditions. Here’s how my erroneous thoughts went: suppose such an F were to exist. Property 2 gives us then that $\frac{qF(t)}{t} \leq F'(t)$ . Solving this “differential inequality” gives us that $F(t) \geq A_1t^q$ . A similar calculation will also yield that $F(t) \leq A_2t^p$ .

Now as a “back of the envelope” calculation, I tried plugging the bounds of F into property 1. Specifically, first I computed

$\int_0^{\infty} A_1qt^{\frac{q-1}{m-1}}dt$ .

Since q<m, the exponent is (strictly) smaller than 1, and the integral diverges (the indefinite integral looks like $ct^{\alpha}$ , where $0<\alpha < 1$ ). In particular, it does great from 0 to any finite number, but has a “fat tail”. Similarly, the integral $\int_0^{\infty} A_1qt^{\frac{p-1}{m-1}}dt$ diverges, but this time because its singularity near zero is too big (the indefinite integral is the same as the previous one, though now $\alpha < 0$. So this one does great from a very small number to infinity, but ultimately diverges.

Possibly I’ve given away the answer since I have emphasized my mis-steps, but here is an example of a Young function satisfying the first two properties. The trick is to construct the function out of two pieces:

The constructed Young function, near where the two "pieces" join.

$F(t) = c_1 t^q$ for small t, and $F(t) = c_2t^p$ for large t. You can even select $c_1, c_2$ so that the derivative is continuous. Explicitly, suppose m = 3. Then we may set F(t) = t for t < 1, and $F(t) = \frac{t^5+4}{5}$ for $t\geq 1$ . Notice that F(t) is continuously differentiable, and that $\int_0^{\infty}F'(t)^{-\frac{1}{m-1}}~dt = 2+1 = 3$ , so we know that $C(3,1,5) \geq 3$ .

Slices followup

Feb9

More from yesterday. Of course I see the following .gif in the course of my daily reading, which blows all my animations out of the water:

This is a sequence of 2-D slices of the human body, collected from the Visible Human Project. For those who don’t go to the wikipedia page, this data was collected in a much more… invasive manner than the MRI I described yesterday. Specifically, a cadaver was “frozen in a gelatin and water mixture”, then they grinded away 1mm, take a picture, and repeat. There is also a female data set with 0.33mm resolution. Also, apparently this guy was a Texan murderer, which is a far less pleasant tie-in than, say, Tibor Rado being at Rice before solving Plateau’s problem, or Milgram being at Syracuse before proving his theorem.

There is also a fantastic viewer for this dataset hosted here.

In any case, this sort of image is a good introduction to the next logical place I was going to go with visualizing data. That is, keeping track of five dimensions of data at once. Yesterday’s images had three spatial dimension and one color dimension. Today’s .gif has two spatial dimension, one color dimension, and one time dimension.

Long exposures and fire: another way to "see" another dimension.

This suggests (and I plan to provide examples of this) having three space dimensions, one color dimension, and one time dimension. A great example would be watching a person’s temperature change over time, or how hot an oven is over time. For today though, we have two somewhat boring examples, in that the color and time dimensions are equal to each other (i.e., I colored these by recording the height, and making that the intensity.

This first is an implementation of a variant of the heat equation with “random shocks” introduced, and Von-Neumann boundary conditions (which means: no energy escapes the system). It is meant to model how head would travel, and the “random shocks” are small points of heat introduced into the system.

The second image is an implementation of a variant of the wave equation (in both these cases, when I say “variant”, I am allowing just a little bit of energy to leave the system so that there is not too much “heat” at the end of the simulation… things tended to just white-out without this). The von Neumann boundary conditions are much more evident in this one, where you can see waves “bouncing” off the walls.

How to solve a variational problem, II

Feb7

Lots of text today = lots of filler photos. Some ducks from the park next door to Rice.

This is a method used to show that a minimizer exists for a variational problem, though it typically provides no clues as to what the minimizer is. It is typically referred to as “the direct method in the calculus of variations”. See yeseterday’s post, at least the first paragraph or two, for background.

First, a point I forgot about yesterday since it is such a convention: “why minimization?” I would guess this is motivated by physics, and has been explored by Hildebrandt and Tromba in The Parsimonious Universe– roughly, that nature seeks to minimize (rather than maximize) energy spent. So much of math has been motivated by physics (often useful, as it provides an intuition as to what should be true), it is only natural many of our questions are posed in this manner. This parsimony can also explain why we typically make sure that the Lagrangian is nonnegative- since energy is nonnegative.

From xkcd. We take the second path here.

Now, the direct method, along with intuition of how we find a least area surface given a prescribed boundary, and what could go wrong in general. We denote the area of a surface u by F[u]:

Geometry? A bridge in upstate New York?

Show that there is at least one candidate minimizer. For the least area surface, we pick a point not on the boundary, and draw a straight line from that point to each boundary point to make our first candidate. As a silly example of what could go wrong, consider trying to minimize the integral of |u|, subject to u(0) = 1 and u(0) = 2. Well, we just cannot satisfy that boundary condition with any function.

2. Take an infimum. We now have a nonempty set of candidates $\{ u_{\alpha} \}$ , which is associated with a nonempty set of real numbers $\{F[u_{\alpha}]\}$ . Going back to the physics explanation, I’ll assume that the integrand is bounded below by zero, and invoke a property of the real numbers to say that there is a greatest lower bound. It will be our goal to find a surface realizing this infimum. Notice though that this step is not constructive, so right here we lose our chance at finding a minimizer analytically. Really the only thing that could go wrong is if our integrand is not bounded below. It would be somewhat silly to try to find the function whose integral is the “most negative”.

Once we have an infimum, M, we can take a sequence of candidates $\{u_j\}$ which converge to the infimum, $F[u_j] \to M$ . Notice that the candidate functions do not necessarily converge to anything. Yet.

"Bikeman" in some of the most beautiful woods in the world.

3. Invoke compactness. Now, lurking under the surface has been this “space of admissible functions”. Often this is a Sobolev space, which has the property that the unit ball is “(weak-*) compact”. See this short paper (pdf link) by Frank Morgan on compactness, which he called “the most important concept in mathematics”. Compactness implies that every bounded sequence has a convergent subsequence. Here “bounded” means “with respect to the norm on the space”. In the case of area minimizers, there is a “mass norm” on the admissible functions (“integer rectifiable currents”) which measures the surface area, and a famous (for some value of the word “famous”) compactness theorem for these functions (defining a space of admissible functions that was physically relevant and so that such a theorem existed was, perhaps, the most difficult part of Plateau’s problem). Hence, we now have a subsequence $\{u_{j'} \}$ , and a target (admissible) function u so that $u_{j'} \to u$ and $F[u_{j'}] \to M$ , still.

A sequence of functions converging to the infimum for the integral of |u(x)| subject to u(0) = 0, u(1) = 1. However, there is no smooth function that they are converging to. This sequence appears on the cover of Frank Morgan's real analysis text.

Last thing to show is that F[u] = M. The two conditions we’ve established certainly nod suggestively at this last equation, but don’t give it themselves. The figure at right shows what could go wrong.

4. Lower semicontinuity of the functional. We need to show that F[u] = M. A typical approach is to prove that the functional is lower semicontinuous. That is to say, $F[\liminf u_j] \leq \liminf F[u_j]$ (fun story: when I asked my advisor to define “upper semicontinuity”, he gave me the finger. Bonus points if you can see why this is a reasonable definition). If this is true, then we have $M \leq F[u] = F[\liminf u_j] \leq \liminf F[u_j] = M$ , and are done. The surface area is lower semicontinuous, which is how we complete the proof of the existence of area minimizing surfaces.

Reusing figures! Non lowersemicontinuity.

The Takagi curves from yesterday provide an example of a functional which is not lower semicontinuous, since $F[u_j] \to 0$ , but $F[u] = 1$ .

How to solve a variational problem, I

Feb6

Only had 5 figures and 600 words, so here's a photo of a saddle in the Guadalupe Mountains. I like that you can see all the "local maxima" easily. If you look closely, you can even see a trail crossing right at the lowest point of the saddle.

Last week, I discussed how to solve a PDE. This week, I want to talk about how to solve a variational problem. By variational problem, I will mean minimizing an integral like

$F[u] = \int_U L(Du,u,x)~dx,$

subject to some boundary conditions, where U is a subset of some Euclidean space, u is the function we are solving for (which maps from U to some other Euclidean space), and Du is the differential of u. If $u: U \subset \mathbb{R}^m \to \mathbb{R}^n$ , then Du is an n x m matrix (though for a real valued u, i.e. where n =1, it is customary to write Du as a row vector, column vectors being hell for typesetting).

Today I focus on examples of variational problems which can be solved analytically, while tomorrow will be an outline of the so-called “direct method in the calculus of variations”.

One minimizer of the integral of u'(x). Any function would do.

First, a variational problem which is (hopefully) easily solved by any student of calculus: Find a function $u: [0,1] \to \mathbb{R}$ which minimizes $\int_0^1 u'(x)~dx$ , subject to u(0) = a, u(1) = b.

In this case, we know that any function that starts at a and ends at b will be a minimizer, since, by the fundamental theorem of calculus,

$\int_0^1u'(x)~dx = u(1)-u(0) = b-a.$

Hence, we have existence, but not uniqueness.

The most famous variational problem is surely minimizing surface area (or length, or volume depending on the dimension of the domain) of a graph. That is, finding a real valued function u that minimizes

$\int_U \sqrt{1+|Du|^2}~dx$

subject to some boundary conditions.

The *only* function that minimizes length, with u(0) = a, u(1) = b.

Longtime reader(s) will recall the Euler-Lagrange equationswhich can sometimes provide a solution to such problems:

$\left. D_uL(Du,u,x)-div_x(D_pL(Du,u,x))=0 \right.$ .

As an easy example, if we wanted to minimize the length of a line, we would use the above functional, Du = u’ in this case (the ol’ 1 x 1 matrix), and the Euler-Lagrange equations give

$\frac{d}{dx}\left( \frac{u'(x)}{\sqrt{1+(u'(x))^2}} \right) = 0$ .

Rather than calculate this derivative, we notice that this means

$\frac{u'(x)}{\sqrt{1+(u'(x))^2}} = C$

$u'(x) = \frac{C}{\sqrt{1- C^2}} = D.$

Hence, u’ is a constant, and our solution must be a straight line, u(x) = Dx+E.

We also point out that it should be surprising that there are any general results for solving variational problems. This post was inspired by Leonid Kovalev’s discussion of the Takagi curve, which is a fractal whose iterates look like a famous counterexample. Specifically, suppose we wish to minimize

$\int_0^1 u(x)^2+(1-|u'(x)|)^2~dx,$

subject to u(0) = u(1) = 0. Notice that the integrand is

Takagi curves

Always nonnegative,
small when u is close to 0,
small when u’ is close to +1 or -1,
only 0 if u is (almost) always 0 and |u’| is (almost) always plus or minus 1.

The sequence of functions pictured at the bottom of the post (which forms the Takagi curve) will always have 0 for the derivative part, and will be getting smaller and smaller on the $u(x)^2$ part of the integrand. In fact, if you name any very small number $\epsilon > 0$ , we can choose a member of this sequence so the integral that is smaller than $\epsilon$ . But there is no function where the integral of this Lagrangian is zero, so there is no minimizing function for this particular Lagrangian!

A sequence of functions, where the integrals of the Lagrangians converge to zero, but there is no limit where the integral of the Lagrangian is zero.

As an aside, I’m sure that this Lagrangian is named/famous, but I could not find mention of it in any of my usual sources…

MATLAB code to generate the above gif. Remove the “pause” commands to just plot everything at once:
function takcurves(n) %generates n iterates of the Takagi curves ColOrd = hsv(n); figure(1) set(gcf, 'Position', get(0,'Screensize')); hold on pause(0.4) for j = 1:n x = 0:.5^j:1; y = zeros(size(x)); y(2:2:size(y,2)) = .5^j; line(x,y,'LineSmoothing','on','Color',ColOrd(j,:)) hold on pause(0.4) end hold off end

How to solve a PDE

Jan26

I briefly considered trying to make the case that smoke was governed by PDEs. Really, I just like this photo.

So here’s an attempt to summarize how to prove that a solution exists for linear, second order partial differential equations. This is some of my favorite mathematics, though at first I was really turned off by all this talk about Sobolev spaces and functional analysis, instead of just solving the darn thing. So I encourage those who have never seen any PDE theory yet to dig in (though maybe some ODE familiarity would be helpful). Unfortunately, I could not come up with any helpful figures/pictures for today (suggestions welcome!), so you get a potpourri of shots.

First, let me define a second order linear differential operator L, but let me do so by describing what it does to a function $u: \mathbb{R}^n \to \mathbb{R}$ (since a second order linear operator is just something that eats functions and gives back functions, in a linear manner):

$Lu = -\sum_{j,k = 1}^n (a^{j,k}(x)u_{x_j}(x))_{x_k} + \sum_{j = 1}^n b^j(x)u_{x_j}(x) + c(x)u(x).$

The photos on the page are mine. The dog, unfortunately, is not.

One famous example of such an operator is the Laplacian, denoted $\Delta$ , for which $a^{j,k}$ is 1 when j = k, and 0 otherwise, and $b^j$ s and c are zero. Put more simply, the Laplacian is the sum of the pure second derivatives. Now we provide first an outline, and then a few details of a proof of existence of solutions.

How to solve Lu = f:

1. Associate to the operator L a bilinear form B. That is, a function B that eats two functions and gives a number which is linear in each coordinate.
2. Remember from functional analysis that, under certain conditions, there exists a unique u so that $B[u,v] = \lambda(v)$ for any v, where $\lambda$ is a linear functional (eats functions, gives a number).
3. Define $\lambda(v) := \int f(x) v(x)~dx$ .
4. Pat yourself on the back for defining B in a clever way so that the u produced actually solves Lu = f in a weak sense.

Again, with slightly more detail:

1. We’ll define
$B[u,v]:=\int\left(\sum_{j,k = 1}^na^{j,k}u_{x_j}v_{x_k}+\sum_{j = 1}^nb^ju_{x_j}v+cuv\right)dx,$

It's a fish!

where everything is a function of x, but that really clutters up the equation. A reason you might have thought to do this yourself is that it takes a little pressure off of u. That is, we only need to require that u has one derivative, and that derivative only has to be defined under an integral sign. If u happened to have two derivatives, we could integrate the first term by parts, and then we would have $B[u,v]=\int Lu\cdot v~dx$ . In this beautiful, integrable, differentiable world, if we could show that $\int Lu \cdot v~dx = \int f \cdot v~dx$ for all functions v, then it would be reasonable to conclude that Lu = f.
2. The Lax-Milgram theorem says, roughly, that if H is a Hilbert space, then for a bilinear form $B: H \times H \to \mathbb{R}$ and a (continuous) linear functional $\lambda: H \to \mathbb{R}$ , there is a unique $u \in H$

Again, I could make the case that gravity is a differential equation, whose solutions are parabolas...

so that $B[u,v]=\lambda(v)$ for each $v \in H$ . There are some other non-trivial hypotheses on B, which may be translated into hypotheses on L, but let’s revel in success now.
3.-4. These steps were actually described pretty well above.

So we need functional analysis to use this great Lax-Milgram theorem. We need Sobolev spaces because our favorite function spaces from calculus- $C^m$ , the m-times differentiable functions- are not Hilbert spaces. Certain Sobolev spaces are, though, and they provide precisely the integrability conditions we need to get precise conditions to guarantee solutions for large classes of PDE.

The 100 words/picture is tough sometimes, but other times I get to put artsy photos in, so everything balances out.

Riddles.

Jan13

At a conference in Palo Alto, heard a few clever riddles:

Suppose you have a 15 x 20 sheet of chocolate. What is the least number of sheets you must break to have only 1 x 1 pieces of chocolate left?
Suppose you are blindfolded, and sitting in front of a table with 40 tiles on it. Each tile is black on one side and white on the other. You are told that precisely 10 of the tiles is turned white side up. You are asked to split the tiles into two groups, each with the same number of white tiles. Further, you are allowed to flip some tiles if you would like (though, remember, you are blindfolded). How do you do this?

Also, to satisfy my mathematically curious reader(s), a speaker at the conference yesterday was discussing “optimal Lipschitz extensions”. Roughly, the question is this: if you have an open, bounded region in $\mathbb{R}^n$ , with a Lipschitz function defined on the boundary, is there a “best” Lipschitz function defined on the entire region? By “best”, we’ll mean that on any open bounded subset, the function has the smallest Lipschitz constant given its boundary.
For example, these two graphs are both Lipschitz with the same boundary data, though the second graph has very small crinkles in it. Really, we are trying to define a notion of “best” that will choose the first extension, but not the second one. It should not be obvious that such an extension even always exists, since we are imposing a number of conditions on the map, or if it exists, that there is only one (existence, in fact, does not hold for vector-valued functions). In any case, there has been some research done into this, but the speaker mentioned a proof of the existence and uniqueness of such extensions using a game theoretic proof (pdf link to the paper by Peres, Schramm, Sheffield and Wilson). This is great.

How it goes is that you choose a point x in the interior of the region, and then have two players playing the following game. A (fair) coin is flipped, and the winner gets to move the point by a certain fixed distance d. The game ends when the point reaches the boundary of the region, at which point player 2 pays player 1 the value of the function on the boundary. Intuitively, player 1 will steer towards high values, and player 2 will steer towards lower values. Now if each player plays optimally, then you can calculate an expected payoff for player 1 at each value x (that is, the average payoff as one plays the game over and over again). As d approaches zero, this expected payoff converges to a value that will define the optimal Lipschitz extension. I think this is a fantastic result.

Back to Houston on Saturday.

Analysis in metric spaces.

Jan8

Heading off today for a conference on mapping theory in metric spaces. The hope is to generalize some results from my dissertation to metric spaces (rather than Euclidean spaces). I thought I might share some thoughts so that one can start thinking about the possible difficulties of analysis in metric spaces.

First, a metric space is just a set of points M together with a metric d that takes two points and returns a distance between them. The function d must have a few properties, which make intuitive sense: distance is a positive number, the distance from a to b must be the same as the distance from b to a, the distance from any point to itself is zero, and there must be a triangle inequality. The triangle inequality just says that there are no shortcuts: the distance from a to b is less than the distance from a to c plus the distance from c to b. ( $d(a,b) \leq d(a,c)+d(c,b)$ )

An easy example is the plane, together with normal Euclidean distance. A great collection of an example that is not a vector space would be a graph (in the sense of a collection of nodes and lines connecting those nodes, rather than the graph of a function). In this case, the distance is the length of the shortest path between two nodes on the graph. This also displays some of the difficulties in working with metric spaces. In particular, given two points on a graph, there is no obvious way of adding those points.This problem becomes more pronounced when, for example, one tries define the derivative of a real valued function on a graph. A way of doing this is to try to keep important properties of the operator. For example, the Laplacian tends to smooth out a function, and so a reasonable definition will be to average a node with its connected nodes. More information can be found at this article. The gif on this page is a randomly generated graph being evolved according to the heat equation, with some random heat shocks thrown in. I’m not entirely happy with the figure, since the x-y coordinates are meaningless, but the z coordinates represent the heat of a node at time t.

Formalism: easy and useful vs. correct

Jan3

A common problem in teaching is, I think, telling the [whole] truth vs. actually teaching something. I have two examples of this problem that have been gnawing at my math conscience for a while:

Separable differential equations:

This is right out of the first day of an ODE course. We look at a separable differential equation which, I am sure you recall, looks something like $y' = xy$ , then write it using Leibniz notation (which is more precise, at the expense of being somewhat intimidating… a topic for another time!) as

$\frac{dy}{dx} = xy.$

We collect all the terms involving y on one side, and all the terms involving x on the other (the ability to do so may be taken as the definition of a separable equation):

$\frac{dy}{y} = x~dx,$

then integrate

$\int \frac{dy}{y} = \int x~dx \Rightarrow \log{y} = \frac{x^2}{2}+C \Rightarrow y = Ae^{x^2}.$

Now, dy/dx is not actually a fraction, and on the one hand, you hope a student calls you out on this. But it is a useful formalism that, as far as I can tell, everyone uses. The true derivation of the above solution should go:

$\frac{1}{y}y' = x \Rightarrow \int \frac{1}{y} y'~dx = \int x~dx \Rightarrow \int \frac{1}{u}~du = \int x~dx,$

then we proceed at usual. I am using the variable u in the third equation to emphasize the change of variables $u = y(x)$ , so $du = y'(x)~dx$ (which again is some formalism that I will duck for now).

In practice, I will not present the second derivation, since the point of the lecture is to learn how to solve separable equations, not to practice changing variables. However, I will encourage students to call out the hand-waving in the first derivation. In a perfect world, I would hope students could justify everything that happens in class, but the last thing I would want to do on the first day of classes is overwhelm students for my mathematical conscience.

Eigenvalues and the trace/determinant:

The other situation where I have often felt mathematical-moral-twinges is when eigenvalues make an appearance in a linear algebra course. Two enormously useful identities for checking that you, at least, might have gotten the eigenvalues right is that the product of the eigenvalues is equal to the determinant of a matrix, and the sum of the eigenvalues is the trace. The proof is not hard (namely, that a matrix is similar to its Jordan normal form, $P^{-1}AP = J$ , where the diagonal of J is the [are the?] eigenvalues of A, and then recalling that the determinant of a product is a product of determinants, so $det(A) = det(J)$ , and that the trace of similar matrices is the same.) However, Jordan normal form comes, necessarily, later than eigenvalues, and I have never had time to go back to present a complete proof.

I have given students this identity with a “cheat code” caveat in the past. That is to say, I will not test them on it, and they cannot use it as justification for calculations, but I point out it would be foolish not to use it to double check calculations: if they get an eigenvalue calculation wrong on the final, I’m not mad, I’m just disappointed.

I am sure there are other examples of topics where this is dealt with, but these have bothered me the most!

Variational thoughts

Thoughts about math or whatever is interesting this day, with a picture every 100 words. Updates M-F.

Category Archives: differential equations